现代博弈理论由匈牙利大数学家冯·诺伊曼于20世纪20年代开始创立

　　博弈论是研究决策者在相互竞争或合作的情境中做出决策的数学模型和分析工具。在博弈论中，有两类主要的博弈模型，即零和博弈和非零和博弈。本文将详细介绍这两种博弈模型的概念、特点和应用，并通过历史起源和具体例子来解释它们的重要性和影响。

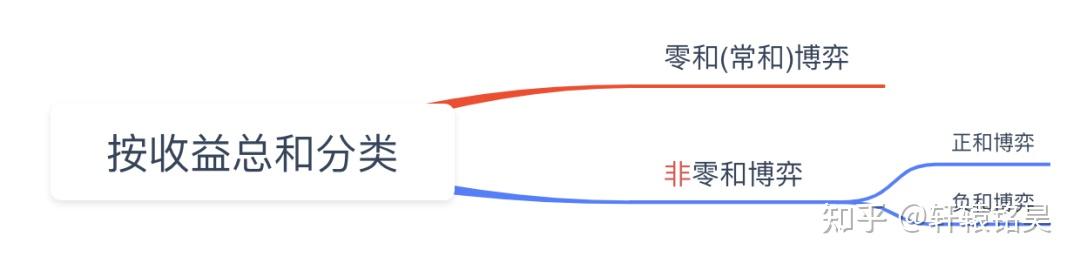
　　零和博弈(Zero-sum game)是博弈论的一个概念，属非合作博弈，指参与博弈的双方，在严格竞争下，一方的收益必然意味着另一方的损失，博弈各方的收益和损失相加的总和永远为"零"，双方不存在合作的可能（完全竞争关系）。零和博弈的结果是一方吃掉另一方，一方的所得正是另一方的所失，整个社会的利益并不会因此而增加一分。由于此模型中参与人的利益总和为零，即一方的利益的增加必然导致另一方的利益的减少。所以，在零和博弈中，参与者之间的冲突和竞争是不可避免的。

　　当你看到两位对弈（下棋）者时，你就可以说他们正在玩"零和游戏"。因为在大多数情况下，总会有一个赢，一个输，如果我们把获胜计算为得1分，而输棋为-1分，那么，这两人得分之和就是：1+（-1）=0。

　　零和博弈的历史起源可以追溯到古代的军事战争和资源争夺。例如，古代国家之间的领土争夺战，当一方扩张领土时，必然导致另一方领土的缩小。这种零和关系在经济领域中也有体现，例如市场竞争中的价格战，一方的价格降低会直接导致竞争对手的销售额减少。

　　这正是"零和游戏"的基本内容：游戏者有输有赢，一方所赢正是另一方所输，游戏的总成绩(收益)永远是零。

　　二人零和博弈的标准式表示如下：甲 \ 乙Choice 1Choice 2Choice 1(-A, A) ∑(-A, A)＝0(B, -B) ∑(B, -B)＝0Choice 2(C, -C) ∑(C, -C)＝0(D, -D) ∑(D, -D)＝0

　　注:第一个数字表示甲的支付（收益），第二个数字表示乙的支付

　　零和博弈源于博弈论，现代博弈理论由匈牙利大数学家冯·诺伊曼于20世纪20年代开始创立，1944年他与经济学家奥斯卡·摩根斯坦合作出版的巨著《博弈论与经济行为》，标志着现代系统博弈理论的初步形成。

　　零和博弈之所以广受关注，主要是因为人们发现社会的方方面面都能发现与"零和博弈"类似的局面，胜利者的光荣后往往隐藏着失败者的辛酸和苦涩。从个人到国家，从政治到经济，似乎无不验证了世界正是一个巨大的零和博弈场。这种理论认为，世界是一个封闭的系统，财富、资源、机遇都是有限的，个别人、个别地区和个别国家财富的增加必然意味着对其他人、其他地区和国家的掠夺，这是一个邪恶进化论式的弱肉强食的世界。我们大肆开发利用煤炭石油资源，留给后人的便越来越少；不断污染环境，带给后人的不良影响便越来越多。

　　通过有效合作皆大欢喜的结局是可能出现的。但从零和博弈走向双赢，要求各方面要有真诚合作的精神和勇气，在合作中不耍小聪明，不要总想占别人的小便宜，要遵守游戏规则，否则双赢的局面就不可能出现，最终吃亏的还是合作者自己。

　　从20世纪以来，人类在经历了两次世界大战、经济的高速增长、科技进步、全球一体化以及日益严重的环境污染之后，"零和博弈"观念正逐渐被"双赢"观念所取代。在竞争的社会中，人们开始认识到"利己"不一定要建立在"损人"的基础上。领导者要善于跳出"零和"的圈子，寻找能够实现"双赢"的机遇和突破口，防止负面影响抵消正面成绩。批评下属如何才能做到使其接受而不抵触，发展经济如何才能做到不损害环境，开展竞争如何使自己胜出而不让对方受到伤害，这些都是每一个为官者应该仔细思考的问题。有效合作，得到的是皆大欢喜的结局。从零和走向正和，要求各方要有真诚合作的精神和勇气，遵守游戏规则，否则"双赢"的局面就不会出现，最终吃亏的还是合作者自己。

　　零和博弈在经济学和国际关系中有广泛的应用。在经济学中，零和博弈常常用于分析市场竞争、价格战和资源分配等问题。例如，两个公司在同一市场上竞争销售同类产品，它们的市场份额和利润之间存在零和关系。一方的市场份额增加，必然导致竞争对手的市场份额减少。

　　国际关系中的零和博弈也十分显著。例如，两个国家之间的贸易争端，一国的出口增加可能导致另一国的出口减少，形成零和关系。此外，核武器军备竞赛也是典型的零和博弈，一方的军备增加可能引发对方的军备扩展，增加了潜在冲突的风险。

　　非零和博弈是一种（非完全竞争）博弈模型，其中参与者之间可以通过合作和互惠来实现互利共赢的结果。与零和博弈不同，非零和博弈中的参与者的利益并不完全对立，而是可以通过合作来达到更好（结果有正和、负和之分，虽然负和会使结果变糟。但按照经济学原理来看，只要存在合作就有机会达到多赢）的结果。

　　非零和博弈的历史起源可以追溯到合作和互惠的概念。在人类社会的早期，人们发现通过合作和互相帮助可以取得更好的生存和繁衍结果。这种合作策略在经济和社会领域中得到广泛应用。

　　二人非零和博弈的标准式表示如下：甲 \ 乙Choice 1Choice 2Choice 1(A, B) ∑(A, B) ≠ 0(C, D) ∑(C, D) ≠ 0Choice 2(E, F) ∑(E, F) ≠ 0(G, H) ∑(G, H) ≠ 0

　　注:第一个数字表示甲的支付（收益），第二个数字表示乙的支付

　　非零和博弈在商业和市场竞争中有重要的应用。例如，企业之间的合作和联盟可以带来共同的市场优势，通过资源共享和技术合作来降低成本和提高竞争力。此外，企业与消费者之间的互惠关系也是非零和博弈的体现，通过提供优质产品和良好的服务来建立长期的合作关系。

　　在国际合作中，非零和博弈的概念也起着重要的作用。例如，多个国家之间的环境保护合作，通过共同努力来减少污染和保护生态环境，实现共同的利益。国际贸易合作也是非零和博弈的典型案例，通过互利共赢的贸易关系来促进经济发展和繁荣。

　　"囚徒困境"的合作策略和多人博弈是非零和博弈的典型例子。在"囚徒困境"中，如果两个犯罪嫌疑人能够相互合作，他们可以达成共同的利益，获得较轻的刑罚。而在多人博弈中，参与者之间可以通过合作和策略的选择来实现最佳结果，而非仅仅追求个体的最大利益。

　　零和博弈和非零和博弈是博弈论中两种重要的博弈模型。零和博弈强调的是竞争和利益的对立，而非零和博弈则强调合作和互惠的重要性。在实际生活和各个领域中，这两种博弈模型都有着广泛的应用，对于决策者和策略制定者来说，理解这些模型的特点和应用，能够帮助做出更明智的决策，实现最佳的结果。